알고리즘 에라토스테네스의 체, 소수, 소인수분해

2020-10-29

1. 소수(Prime Number)

1.1. 소수의 정의

소수란 약수가 1과 자기 자신밖에 없는수를 일컫는 말입니다.

1.2. 소수의 특징

N이 소수가 되려면 2<= N <= N-1 2보다 크거나 같고, N-1보다 작거나 같은 자연수로 나누어 떨어지면 안됩니다.
그 이유는 N의 약수중에서 가장 큰것은 N/2보다 작거나 같기 때문입니다.
N = a * b 로 나타낼 수 있는데, a가 작을 수록 b값이 크게 됩니다.
가능한 a 중에서 가장 작은 값은 2이기 때문에 b는 N/2를 넘지 않습니다.
두 수 a와 b차이가 가장 작은 경우는 루트 N이기 때문에 루트 N까지만 검사를 진행하면 됩니다.
어떤 수 N이 소수인지 아닌지 알아내는데 걸리는 시간 복잡도는 O(루트N)이었다.
N= 백만일 경우: 루트 N=1000, N=1억인 경우: 루트 N=10000

만약, 1부터 1,000,000까지 모든 소수를 구하는데 걸리는 시간복잡도는 어떻게 될까요?

각각의 수에 대해서 소수 인지 아닌지를 검사해야합니다. 판별만 하는데 사용되는 시간복잡도: O(루트N)
수는 총 N개이기 때문에 모든 소수를 구하는데 걸리는 시간복잡도는 N*O(루트N)의 시간이 소요됩니다.
즉 N이 1,000,000 백만이라고 가정하였을때 시간복잡도는 1,000,000 * 1,000 = 1,000,000,000 = 10억 = 10초라는 시간이 걸리게 됩니다. 이는 1초에 1억을 연산하는 시간복잡도를 생각하였을때 큰 시간이 필요하게 됩니다.

소수의 예시

1-100까지의 소수
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97

소수 판별 기본 함수

bool prime(int num){
    if(n <2){
        return false;
    }
    
    for(int i=2; i<=n-1; i++){
        if(num % i == 0){
            return false;
        }
    }
}

num값이 i로 나누어 떨어지는 값이 0일 경우 소수가 아닙니다.

소수 루트 N까지 진행하는 함수

bool prime(int num){
    if(n <2){
        return false;
    }
    
    for(int i=2; i*i<=n; i++){
        if(num % i == 0){
            return false;
        }
    }
}

루트 i<=N은 i<= NN과 같이 나타내 수 있으며 즉, 루트 N은 ii, i^2으로 나타낼 수 있다.
어떤 수 N이 소수인지 아닌지 판별만 하는데 걸리는 시간복잡도는 O(루트 N) 입니다.
모든 소수를 구하게 되면 N * O(루트N)의 시간 복잡도를 갖는다는것에 유의해야합니다.

지워지지 않은 수를 찾을 때 n이 아니라 sqrt(n) 까지만 찾습니다. i의 배수들을 지울 때 2 * i 에서 시작하는 것이 아니라 i * i 에서 시작한다. 2 * i에서 2의 배수 들은 모두 지워졌을 것이고 3 * i 는 3의 배수를 지울 때 이미 지워졌을 것입니다.

2. 에라토스테네스의 체(Sieve of Eratosthenes)

2.1. 에라토스테네스의 체 정의

위에서 확인한 바와 같이 1~1,000,000까지 모든 소수를 구하기 위해서는 많은 시간이 소요되는것을 확인하였습니다. 이것을 해결하기 위해서 에라토스테네스의 체를 사용하면 해결 할 수 있습니다.

에라토스테네스의 체 원리

에라토스테네스의 체 원리

1. 2부터 N까지 모든 수를 써놓는다.
2. 아직 지워지지않은 수 중에서 가장 작은수를 찾는다.
3. 그 수는 소수이다.
4. 이제 그 수의 배수를 모두 지웁니다.

과정

1. 지워지지 않은 수 중에서 가장 작은 수는 2이다.
2. 2는 소수이고 2의 배수를 모두 지웁니다.
3. 3의 배수를 지웁니다.
4. 5의 배수를 지웁니다.
5. 7의 배수를 지웁니다.
6. 11의 배수는 이미 지워져있습니다. 이미 2,3,5,7의 배수를 지우는 과정에서 지워졌기때문입니다.
7. 11*11은 특히 121로 100을 넘어가기 때문에 더이상 수행할 필요가 없게 됩니다. 따라서, 남아 있는 모든 수가 소수가 되게 됩니다.

/*소수 저장*/
int[] prime = new int[101];
/*소수의 개수를 저장하기 위한 변수*/
int prime_num = 0;
/*소수가 지워졌으면 true*/
boolean[] check = new boolean[101];
/*100까지의 소수*/
int n = 100;

for(int i=2; i<=n; i++){
    if(check[i] == true){
        continue;
    }
    
    prime[prime_num++] = i;
    for(int j=i+i; j<=n; j+=i){
        check[j] = true;
    }
}

여기서 잘보면 i*i 대신 i+i 부터 시작하는것을 볼 수 있는데, 그 이유는 i가 백만일 경우 i*i를 하게되면 범위를 넘어서게 됩니다. 예를 들면 백만 * 백만 일 경우 10^12가 되기 때문에 오버플로우에 대해서 생각을 할 수 있어야합니다. 총 10^12까지 진행되므로 int형 자료형의 범위인 21억까지 진행하기가 힘들 것으로 판단할 수 있어야합니다. 그리고, long의 범위로 변경하여 진행하여야합니다.

int 자료형: 2,147,483,646
long 자료형: 9,223,372,036,854,775,806

따라서, 21억 이상을 표현하려면 long형이 필요하다는것을 알 수 있어야합니다.

이것을 자바로 표현하였을때는 Long.parseLong 함수를 사용하여 long의 범위를 Long의 형태로 바꾸어줄 수 있습니다.

1	Long.parseLong("9999962000357");

3. 소인수 분해(prime factorization)

3.1. 소인수분해 정의

소인수분해란(prime factorization, integer factorization)?

합성수를 소수의 곱으로 나타내는 방법을 말합니다. 소수의 곱으로 나타낼 수 있는 값을 합성수라고 합니다.
즉, N이 4일 경우 소수 2를 두번곱해서 만들 수 있는 값이 되는 것입니다. N이 합성수가 되고 2는 소수가 되게 됩니다.

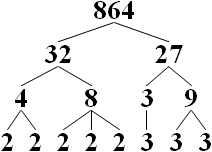
소인수분해 그림

다음 아래는 합성수의 소인수 분해의 예시를 가져왔습니다.

4＝2×2
6＝2×3
8＝2×2×2
9＝3×3
10＝2×5
12＝2×2×3
14＝2×7
15＝3×5
16＝2×2×2×2
18＝2×3×3
20＝2×2×5
21＝3×7
22＝2×11

아래문제는 직접 만들어본 문제입니다.

3.2. 합성수가 주어지면 소수의 곱으로 나타낼 수 있는 숫자를 구하시오. 단, 1<= N <= 1,000,000

자료형 접근

소인수분해 가정에서 가장 중요하게 생각해야하는점은 i*i를 통해 소수의 값을 가져올때가 문제가 됩니다.
만약 i = 1,000,000일 경우 i * i = 1,000,000,000,000 약 10^12까지 진행이 됩니다. 이럴 경우 int자료형으로는 접근할 수 없고,long타입을 사용해야겠다고 생각을 해야합니다.
위에서 말씀드린바와 같이 아래의 자료형의 범위를 갖게 됩니다. 21억 이상 표현하기 위해서는 long형을 사용합니다.

int 자료형: 2,147,483,646
long 자료형: 9,223,372,036,854,775,806

1 2	long num = Long.parseLong("9999962000357"); long num_tmp = Long.parseLong("9999962000357");

해당 long의 범위를 구하기 위해서 위와 같이 표현하였습니다.

소인수 분해의 원리

2~N까지의 값중에서 N % i 의 값이 0 일때 해당 몫의 값으로 다시 N에 넣어주면서 진행하는것을 뜻합니다. 결국 i의 값이 소인수 분해의 값이고 N>1클 경우 마지막의 값을 출력시킬 수 있습니다.

반드시, sqrt 루트까지 진행하는데 에라토스테네스의체를 진행하면 기존의 N배수는 지워졌을 것이기때문에 Sqrt(N)까지만 진행해도 됩니다… 이것을 코드로 나타내면 i=2; i*i ≤ N; i++으로 나타낼 수 있습니다.

for(long i=2; i*i<=num; i++){
    while(num % i == 0){
        System.out.println(i);
        num = num / i;
    }
}
if(num == num_tmp){
    System.out.println("-1");
}
else if(num > 1){
    System.out.println(num);
}

num == num_tmp의 코드는 기존의 num값이 num % i == 0인 값이 없다는 것을 뜻하고 즉, 소인수 되는 수를 찾을 수 없을때 -1을 출력하는 코드입니다. 그리고 해당 num의 값이 1보다 큰 값을 가지고 있으면 해당 마지막 인수를 출력시켜주는 부분입니다.

3.3. 소스코드

public class 소인수분해 {
    public static void main(String[] args) {

        long num = Long.parseLong("9999962000357");
        long num_tmp = Long.parseLong("9999962000357");
        HashMap<String,Integer> hm = new HashMap<>();
        /*
        long타입을 표현하기 위해서는 Long.parseLong으로 선언한다.
        최적화 방안
        - 지워지지 않은 수를 찾을 때 n이 아니라 sqrt(n) 까지만 찾는다.
        - i의 배수들을 지울 때 2 * i 에서 시작하는 것이 아니라 i * i 에서 시작한다. 2 * i에서 2의 배수 들은 모두 지워졌을 것이고 3 * i 는 3의 배수를 지울 때 이미 지워졌을 테니까.
         */
        for(long i=2; i*i<=num; i++){
            while(num % i == 0){
                System.out.println(i);
                num = num / i;
            }
        }
        if(num == num_tmp){
            System.out.println("-1");
        }
        else if(num > 1){
            System.out.println(num);
        }
    }
}

Algorithm자료구조론